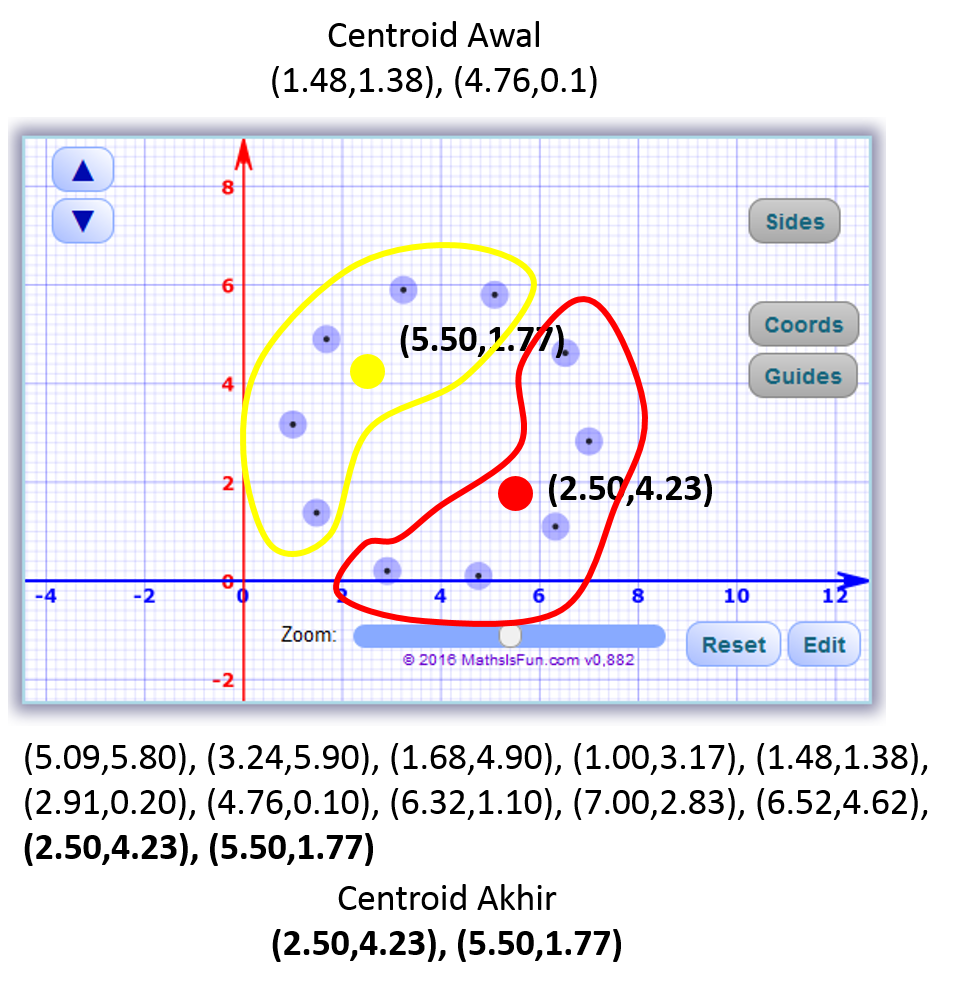
penerapan-k-means-clustering

Penerapan K-Means Clustering pada Multivariate Data

Tidak sedikit yang menanyakan tentang penerapan K-Means, beberapa menanyakan apakah K-Means dapat digunakan pada Multivariate Data ? beberapa diantaranya juga menanyakan apakah bisa digunakan pada data dengan attribut yang banyak ? ada juga yang menanyakan apakah bisa untuk melakukan clustering terhadap data non numerik ? dan beberapa pertanyaan lainnya.

Pada artikel kali ini, khusus penulis akan membahas penerapan K-Means Clustering pada Multivariate Data. Apa itu multivariate data ? adalah data yang memiliki variasi tipe data yang berbeda. Data dapat kita bedakan berdasarkan tipenya, seperti :

  • Quantitative Data / Numerical Data, adalah data yang berupa data angka, baik integer, positive/negative integer, atau pun float/decimal.
  • Binary Data, adalah data yang hanya berisi data 0/1, true/false, ya/tidak, Pria/Wanita, dll.
  • Nominal Data, adalah data yang berisi pilihan, dimana data hanya dapat dipilih satu dari sekian banyak pilihan. Contoh : Dalam pertanyaan dengan pilihan ganda hanya boleh memilih 1 jawaban dari opsi (a, b, c, d), dsb.
  • Ordinal Scale, adalah data yang menyerupai skala atau jangkauan data, dimana data tersebut tidak ada nilai quatitative yang signifikan. Contoh : (Sangat Tidak Setuju, Tidak Setuju, Setuju, Sangat Setuju), atau (Memuaskan, Sangat Memuaskan, dan Dengan Pujian), dsb.

    • Setelah mengetahui tipe datanya, mari kita langsung ke pokok diskusi. Berikut dibawah ini adalah data sample yang saya miliki.

    Sample Data
    Nama IPK Semester Kampus Tingkat Kesulitan Kepuasan
    A 3.00 7 ITS Sangat Susah Puas
    B 3.50 5 ITB Susah Sangat Puas
    C 3.40 3 UGM Gampang Puas
    D 3.80 6 ITS Gampang Sangat Puas
    E 3.00 7 UI Sangat Susah Tidak Puas
    F 3.40 5 ITB Susah Puas

    Akan dilakukan proses clustering berdasarkan data diatas menggunakan K-Means Clustering. Bagaimana caranya ? caranya adalah dengan melakukan normalisasi data terlebih dahulu. Bagaimana melakukannya ? mari kita ikuti step by step dibawah ini. Penulis juga menyertakan file excel yang diembed disini untuk mempermudah pemahaman teman-teman pembaca.

    Mari kita kupas bersama – sama, mungkin teman – teman pembaca telah melihat sekilas tab Raw Data, dan Vector. Tapi mari kita ikut step by step dibawah ini.

    Hal yang perlu kita lakukan adalah :

  • Mentransformasi data diatas menjadi data vector.
  • Data yang bukan numerik, dibuatkan dummy variabel bila diperlukan.
  • Melakukan normalisasi data dengan menghitung Distance Matrix pada setiap attribute.
  • Terapkan algoritma sesuai dengan data yang dimiliki, bisa menggunakan Euclidean Distance, Hamming Distance, Manhattan Distance, Minkowski Distance, Chebyshev Distance, ataupun algoritma lainnya untuk melakukan normalisasi silahkan riset sendiri 😀 .
  • Buat Aggregate Data.

    • Karena attribut (Kampus, Tingkat Kesulitan, dan Kepuasan) adalah data non numerik. Maka kita perlu membuat dummy variabel berdasarkan rumus : dimana adalah Ceiling Symbol, dimana hasilnya selalu dinaikkan ke nilai integer selanjutnya. Contoh : dv = 2.3  , maka ceil dv = 3 , bila dv = 4.3 , maka ceil dv = 5 , dst. Sedangkan variabel c adalah adalah jumlah kategori dalam data. Contoh : Kampus (ITB, ITS, UGM, UI) ada 4 kategori maka c = 4 , dst.

    Transform Data To Vector
    Kampus ITB ITS UGM UI
    dv1 1 1
    dv2 1 1
    (0,0) (1,0) (0,1) (1,1)
    Tingkat Kesulitan Sangat Susah Susah Gampang Sangat Gampang
    dv1 1 1
    dv2 1 1
    (0,0) (1,0) (0,1) (1,1)
    Kepuasan Sangat Tidak Puas Tidak Puas Puas Sangat Puas
    dv1 1 1
    dv2 1 1
    (0,0) (1,0) (0,1) (1,1)

    Tranformasi data diatas didapat dari pola Binary Table N bit seperti dibawah ini :

    Dummy Variable = n bit binary table
    dvn = 2^n dv3 dv2 dv1
    1
    1
    1 1
    1
    1 1
    1 1
    1 1 1

    Contoh pada Attribut Kampus (ITB, ITS, UGM, UI), maka bila memilih :

  • ITB, nilainya adalah (dv1,dv2) = (0,0)
  • ITS, nilainya adalah (1,0)
  • UGM, nilainya adalah (0,1)
  • UI, nilainya adalah (1,1)
  • Begitu juga seterusnya dengan attribut yang lainnya.

    • Silahkan amati kembali Excel diatas pada tab Raw Data, pahami terlebih dahulu sebelum masuk ke step selanjutnya karena step selanjutnya akan berisi perhitungan – perhitungan matematis. Mudahkan ? Bila sudah dipahami mari kita lanjutkan.

    Setelah data dibuat menjadi vector, maka selanjutnya menormalisasikan data tersebut dan membuat Aggregate Data dari seluruh attribute. Mari kita lihat data kita yang sekarang, seperti yang ditunjukkan oleh tabel dibawah ini :

    Data Setelah di vector kan
    Nama IPK Semester Kampus Tingkat Kesulitan Kepuasan
    A 3.00 7 (1,0) (0,0) (0,1)
    B 3.50 5 (0,0) (1,0) (1,1)
    C 3.40 3 (0,1) (0,1) (0,1)
    D 3.80 6 (1,0) (0,1) (1,1)
    E 3.00 7 (1,1) (0,0) (1,0)
    F 3.40 5 (0,0) (1,0) (0,1)

    Selanjutnya kita akan menghitung Distance Matrix pada setiap attribut data. Karena attribute (IPK dan Semester) adalah numerik, maka penulis akan menggunakan Manhattan Distance.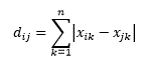

    Selanjutnya, kita hitung Manhattan Distance dari Attribut IPK.

    Manhattan Distance 3 3,5 3,4 3,8 3 3,4
    IPK A B C D E F
    3 A 0,5 0,4 0,8 0,4
    3,5 B 0,5 0,1 0,3 0,5 0,1
    3,4 C 0,4 0,1 0,4 0,4
    3,8 D 0,8 0,3 0,4 0,8 0,4
    3 E 0,5 0,4 0,8 0,4
    3,4 F 0,4 0,1 0,4 0,4
    Max 0,8 Min

    Darimana didapat angka-angka tersebut ? Dari kolom A ke bawah, didapat dari :

  • (A, A) = abs(3 – 3) = absolut(0) = 0
  • (A, B) = abs(3 – 3.5) = absolut(-0.5) = 0.5
  • (A, C) = abs(3 – 3.4) = 0.4
  • (A, D) = abs(3 – 3.8) = 0.8
  • (A, E) = abs(3 – 3) = 0
  • (A, F) = abs(3 – 3.4) = 0.4
  • Dan seterusnya sama halnya dengan attribut Semester.

    • Selanjutnya kita hitung Distance Matrix dari Attribute (Kampus, Tingkat Kesulitan, Kepuasan). Karena attribut tersebut berupa koordinat, maka penulis akan menerapkan Hamming Distance pada ketiganya.

    Hamming Distance (1,0) (0,0) (0,1) (1,0) (1,1) (0,0)
    Kampus A B C D E F
    (1,0) A 1 2 1 1
    (0,0) B 1 1 1 2
    (0,1) C 2 1 2 1 1
    (1,0) D 1 2 1 1
    (1,1) E 2 2 1 1 2
    (0,0) F 1 1 1 2
    Max 2 Min

    Bagaimana formula dari Hamming Distance ? formulanya sebagai berikut :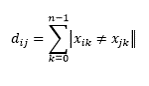Setiap xor data yang bukan 0, atau setiap data x(i,j) ≠ x(j,k)  maka jumlahkan nilainya. Contoh hasil dari attribut Kampus sebagai berikut :

    (A, A) 1
    1
    (A, B) 1
    1
    (A, C) 1
    1
    2
    (A, D) 1
    1
    (A, E) 1
    1 1
    1
    (A, F) 1
    1

    Begitu juga untuk attribut Tingkat Kesulitan dan Kepuasan. Perhatikan kembali Excel diatas pada tab Vector. Silahkan scroll pada excel digeser ke kanan untuk melihat Normalisasi pada setiap attribut. Silahkan di pahami terlebih dahulu excel tersebut kemudian kita lanjut ke step berikutnya.

    Setelah kita hitung Distance Matrix nya, kita buat normalisasi datanya, dengan formula sebagai berikut :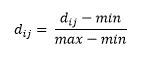

    • (A, A) = (0 – 0) / (0.8 – 0) = 0
    • (A, B) = (0.5 – 0) / (0.8 – 0) = 0.625
    • (A, C) = (0.4 – 0) / (0.8 – 0) = 0.5
    • (A, D) = (0.8 – 0) / (0.8 – 0) = 1
    • (A, E) = (0 – 0) / (0.8 – 0) = 0
    • (A, F) = (0.4 – 0) / (0.8 – 0) = 0.5
    • Dan seterusnya pada kolom dan attribut lainnya.

    Sehingga hasilnya sebagai berikut untuk attribut IPK :

    Normalize Distance
    IPK A B C D E F
    A 0,625 0,5 1 0,5
    B 0,625 0,125 0,375 0,625 0,125
    C 0,5 0,125 0,5 0,5
    D 1 0,375 0,5 1 0,5
    E 0,625 0,5 1 0,5
    F 0,5 0,125 0,5 0,5

    Nilai Aggregate didapat dari jumlah seluruh data yang telah dinormalisasi. Contoh : (A, A) = IPK(A, A) + Semester(A, A) + Kampus(A, A) + Tingkat Kesulitan(A, A) + Kepuasan(A,A)

    Sehingga didapat Aggregate data sebagai berikut :

    Aggregation
    Sum A B C D E F
    A 2,625 4 1,75 1 2,5
    B 2,625 2,625 2,625 3,625 0,125
    C 4 2,625 3,25 3 2,5
    D 1,75 2,625 3,25 2,75 2,75
    E 1 3,625 3 2,75 3,5
    F 2,5 0,125 2,5 2,75 3,5

    Hasil rata – rata data Aggregate :

    Average Distance A B C D E F
    A 0,525 0,8 0,35 0,2 0,5
    B 0,525 0,525 0,525 0,725 0,025
    C 0,8 0,525 0,65 0,6 0,5
    D 0,35 0,525 0,65 0,55 0,55
    E 0,2 0,725 0,6 0,55 0,7
    F 0,5 0,025 0,5 0,55 0,7

    Setelah data diubah menjadi vector selanjutnya data dapat diolah untuk di cluster menggunakan K-Means Clusterig. Silahkan gunakan aplikasi pada link berikut dengan data 

    nxm dimension = 6,2
samples = 0,0.525,0.8,0.35,0.2,0.5,0.525,0,0.525,0.525,0.725,0.025,0.8,0.525,0,0.65,0.6,0.5,0.35,0.525,0.65,0,0.55,0.55,0.2,0.725,0.6,0.55,0,0.7,0.5,0.025,0.5,0.55,0.7,0
centroid dikosongkan saja

    Silahkan dicoba bila dicluster sebanyak 3 atau 4, dsb. Untuk excel embedded silahkan di full view dengan klik ikon pojok kanan bawah excel tersebut.

    Bila ada pertanyaan atau diskusi seputar K-Means Clustering pada Multivariate Data berikut, silahkan komentar. Terima kasih. 😀